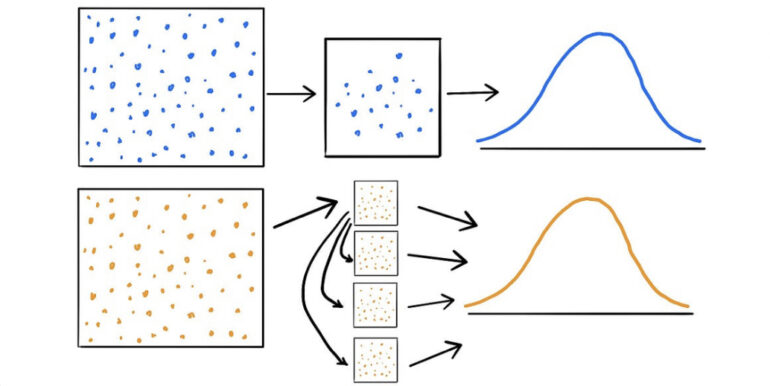
It is a resampling technique naturally used to assess statistics on inhabitants by sampling a dataset with alternatives. It is a valuable tool in applied machine learning for estimating the skill of machine learning models when making predictions on data that were not part of the training set.
One of the desirable properties of using the bootstrap technique to estimate machine learning model skill is the ability to present the estimated skill with confidence intervals, which is not readily available with other methods like cross-validation.
In this tutorial, we will explore the bootstrap resampling technique for estimating the skill of machine learning models on unseen data. By the end of this tutorial, you will gain the following knowledge:
- The bootstrap method involves iteratively resampling a dataset with replacement;
- When using the bootstrap, you need to determine the size of the sample and the number of repeats;
- The scikit-learn library provides a function that facilitates dataset resampling for the bootstrap technique.
Bootstrap Method
The bootstrap technique is a statistical technique that allows us to estimate quantities about a population by averaging estimates from multiple small data samples. This method constructs samples by drawing observations from a larger dataset one at a time and returning them to the dataset after selection. Importantly, this approach enables the inclusion of a single observation in multiple small samples. Such sampling with replacement is a key characteristic of the bootstrap method.
Let’s summarize the process of building one sample using the bootstrap technique:
- Determine the desired size of the sample;
- While the size of the sample is smaller than the chosen size: Randomly select an observation from the dataset / Add the observation to the sample.
The bootstrap method can be utilized to estimate quantities of interest in a population. This involves repeatedly taking small samples, calculating a statistic of interest for each sample, and finally taking the average of the calculated statistics. We can outline this procedure as follows:
1. Select the desired number of bootstrap samples to perform.
2. Choose a sample size.
3. For each bootstrap sample:
- Draw a sample with a replacement, using the chosen size;
- Calculate the desired statistic on the sample.
4. Calculate the mean of the calculated sample statistics.
Additionally, this procedure can be employed to estimate the skill of a machine learning model. This is achieved by training the model on a sample and evaluating its performance on the remaining samples not included in the training set. These excluded samples are referred to as out-of-bag samples or OOB samples for short.
Estimating Model Skill with the Bootstrap Method
The bootstrap technique is a powerful technique for estimating the skill of a machine learning model. By repeatedly resampling the data and evaluating the model on different samples, we can obtain reliable estimates of its performance on unseen data.
Procedure for Estimating Model Skill
To estimate the skill of a model using the bootstrap method, follow these steps:
- Determine the number of bootstrap samples to perform;
- Choose the sample size for each bootstrap sample;
- For each bootstrap sample:
- Draw a sample with a replacement, using the chosen size;
- Fit the model on the data sample;
- Evaluate the model’s skill on the out-of-bag sample.
- Calculate the mean of the sample of model skill estimates.
It is crucial to note that any data preparation and hyperparameter tuning should be done within the for-loop on the data sample. This prevents data leakage, where knowledge of the test dataset is used to improve the model and leads to an overly optimistic skill estimate.
Benefits of the Bootstrap Method
The bootstrap technique offers several useful features for estimating model skills. The resulting sample of skill estimates often follows a Gaussian distribution. This allows us to summarize the distribution using measures of central tendency, such as the mean, as well as measures of variance like the standard deviation and standard error. Moreover, a confidence interval can be calculated to provide bounds for the estimated skill, which is valuable when presenting the performance of a machine learning model.
Configuration of the Bootstrap
When performing the bootstrap, two parameters need to be determined:
- Sample Size: Choose the size of the sample to be used in each bootstrap iteration;
- Number of Repetitions: Decide on the number of times the resampling procedure will be repeated.
Careful consideration of these parameters is essential to ensure accurate and reliable estimates of model skill.
Choosing Sample Size
In machine learning, it is common to use a sample size that matches the size of the original dataset. However, if the dataset is large and computational efficiency is a concern, smaller sample sizes like 50% or 80% of the dataset can be utilized.
Determining Repetitions
The number of repetitions in the bootstrap technique should be sufficient to calculate meaningful statistics such as the mean, standard deviation, and standard error on the sample. A minimum of 20 or 30 repetitions is often reasonable, but smaller values can be used to introduce more variance in the calculated statistics. Ideally, if time permits, it is beneficial to have a larger sample of estimates with hundreds or thousands of repetitions.
Leveraging Bootstrap API
Fortunately, manually implementing the bootstrap method is not necessary. The scikit-learn library offers an implementation that generates a single bootstrap sample of a dataset. The `resample()` function from sci-kit-learn can be employed for this purpose. It takes arguments such as the data array, whether to sample with replacement, the size of the sample, and the seed for the pseudorandom number generator used before sampling.
For example, we can create a bootstrap sample with a replacement containing 4 observations using a seed value of 1 for the pseudorandom number generator.
However, it’s worth noting that the API does not provide a straightforward way to gather the out-of-bag observations, which could serve as a test set for evaluating a fitted model. In the case of univariate data, a simple Python list comprehension can be used to collect the out-of-bag observations.

Extensions
Here are some additional ideas to extend the tutorial:
- List three summary statistics that can be estimated using the bootstrap method;
- Find three research papers that employ the bootstrap technique to evaluate the performance of machine learning models;
- Implement your function to generate a sample and an out-of-bag sample using the bootstrap method.
If you explore any of these extensions, I would love to hear about your findings.
The Importance and Applications of the Bootstrap Method
The bootstrap method is a powerful resampling technique widely used in statistics and machine learning. It provides a valuable approach for estimating statistics and evaluating the performance of models on unseen data. In this section, we will delve deeper into the importance and various applications of the bootstrap method.
Estimating Statistics
The bootstrap method allows us to estimate various statistics of interest, such as the mean, standard deviation, median, and more. By resampling the dataset with replacement, we can generate multiple bootstrap samples and calculate the desired statistic for each sample. The resulting distribution of statistics provides valuable insights into the population parameter we are estimating.
Confidence Intervals
One of the major advantages of the bootstrap method is its ability to compute confidence intervals. A confidence interval provides a range of values within which we can reasonably expect the true population parameter to fall. By calculating the percentile values of the bootstrap sample statistics, we can construct confidence intervals, which offer valuable information about the uncertainty associated with our estimations.
Hypothesis Testing
The bootstrap technique can be used for hypothesis testing, a fundamental aspect of statistical inference. By generating bootstrap samples under the null hypothesis, we can assess the probability of observing certain statistics or test statistics. This allows us to make informed decisions about accepting or rejecting a hypothesis based on the resampled data.
Machine Learning Model Evaluation
The bootstrap method finds extensive applications in evaluating the performance of machine learning models. When training and evaluating models, it is crucial to assess their skill on unseen data. The bootstrap method provides a reliable approach by resampling the dataset and measuring the model’s performance on out-of-bag samples. This helps in estimating the model’s generalization ability and allows us to compare different models effectively.
Model Selection and Validation
In addition to evaluating model performance, the bootstrap method is also valuable for model selection and validation. By creating multiple bootstrap samples and training models on each sample, we can compare their performance metrics and choose the best model. This technique reduces the risk of model overfitting and helps in selecting models that generalize well to unseen data.
Regression and Classification
The bootstrap method is widely applicable in both regression and classification problems. In regression, it enables us to estimate the regression coefficients, evaluate the model’s predictive power, and assess the uncertainty associated with the predictions. In classification, the bootstrap method helps estimate classification error rates, evaluate model accuracy, and assess the stability of feature selection procedures.
Time Series Analysis
Time series data often exhibit complex dependencies and trends. The bootstrap method can be extended to handle time series analysis by considering the temporal aspects of the data. Techniques such as block bootstrapping and stationary bootstrap are commonly used to resample time series data, preserving the temporal correlation structure and providing accurate estimations.
Robustness and Nonparametric Inference
The bootstrap method is particularly useful in situations where traditional statistical methods may not be applicable or assumptions about the underlying distribution are violated. It provides a nonparametric approach to inference, relying on resampling rather than strict assumptions. This makes it robust and flexible in handling a wide range of data types and scenarios.
Model Calibration and Uncertainty Quantification
The bootstrap method plays a vital role in calibrating machine learning models and quantifying their uncertainty. By creating bootstrap samples and training models on each sample, we can obtain a distribution of model predictions. This distribution reflects the inherent uncertainty in the model’s outputs and can be used for uncertainty quantification, decision-making, and risk analysis.
Robust Confidence Intervals
The bootstrap method offers a robust alternative to traditional parametric methods for constructing confidence intervals. It is particularly useful when the underlying data distribution is unknown or does not follow a specific parametric form. The bootstrap approach provides reliable confidence intervals that are not reliant on distributional assumptions and can capture the true uncertainty of the population parameter.
To Wrap Up
In conclusion, the bootstrap method is a versatile resampling technique that finds extensive applications in statistics and machine learning. Its ability to estimate statistics, construct confidence intervals, and evaluate model performance makes it a valuable tool in data analysis. By harnessing the power of resampling, the bootstrap method empowers researchers and practitioners to make reliable inferences and draw meaningful conclusions from their data.
In this tutorial, you’ve explored the bootstrap resampling method, which is a valuable technique for estimating the skill of machine learning models on unseen data.
Here’s a recap of what you’ve learned:
- The bootstrap method involves iteratively resampling a dataset with replacement;
- When utilizing the bootstrap, you need to determine the size of the sample and the number of repetitions;
- The scikit-learn library provides a convenient function for resampling a dataset using the bootstrap method.
If you have any questions, please feel free to ask them in the comments section below. I’ll be happy to provide answers and further assistance.