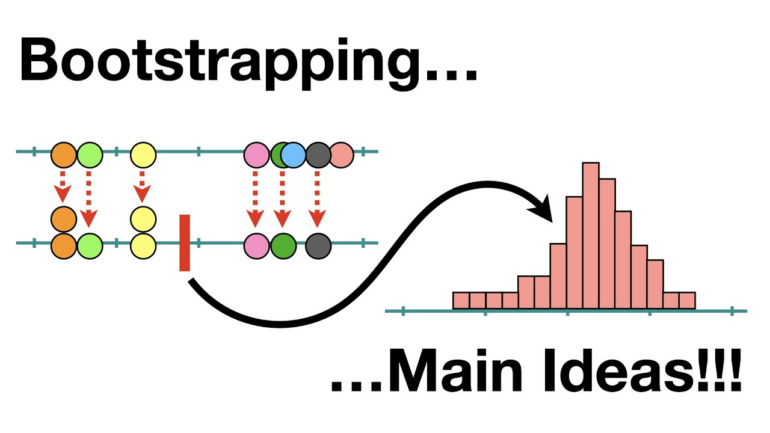
In the world of statistics, obtaining accurate estimates of population parameters is crucial for making meaningful inferences and drawing reliable conclusions. However, this task is often challenging, especially when dealing with limited or incomplete data. Bootstrap statistics, a powerful resampling technique, offers a solution by providing a robust and flexible approach to estimate parameters and assess their uncertainty. In this article, we will delve into the concept of bootstrap statistics, its methodology, and its wide range of applications across various fields.
Understanding Bootstrap Statistics
Bootstrap statistics, also known as bootstrapping, is a resampling approach in statistics that allows us to predict the distribution of the sample of a statistic by randomly sampling individuals from the population itself. It was introduced by Bradley Efron in the late 1970s and has since gained widespread recognition for its versatility and reliability.
The core concept of bootstrapping involves iteratively generating additional pieces through resampling from the original ones to create numerous pseudo-samples. The statistic of interest is then computed on them, allowing us to analyze their distribution. This approach enables the estimation of standard error, construction of estimation bounds, and performance of hypothesis testing, all without the need for conventional assumptions about the population variability.
Methodology of Bootstrap Statistics
The methodology of this kind or statistics can be summarized in the following steps:
- Sample. Begin with a given sample dataset containing “n” observations;
- Resample. Randomly select “n” observations from the primary subset, with substitution. It ensures that each bootstrap sample has the same size as the original one but grants the possibility of repeated observations;
- Calculate statistic. Compute the desired statistic (mean, median, typical deviation, etc.) for each piece of that type;
- Repeat. Repeat steps 2 and 3 again and again (typically thousands) to generate a metrics dispersion;
- Analyze results. Examine the variability of the statistic to estimate its typical error, construct confidence intervals, or perform other statistical analyses.
What Is a Bootstrap Sample in Statistics?
In statistics, a bootstrap sample refers to a resampled dataset created by randomly making observations from the original dataset with substitution. The term “bootstrap” comes from the phrase “pulling oneself up by one’s bootstraps,” as this kind of technique allows us to evaluate properties of a whole from a singular segment without relying on additional assumptions.
When creating it, each observation in the original dataset has an equal chance of being selected and included in the resampled dataset. However, due to the selection process allowing duplication, some instances from the original dataset may be selected repetitively in this sample, while some may not be selected at all. This procedure allows for the possibility of repeated observations and ensures that the size of the resampled subset is the same as the original dataset.
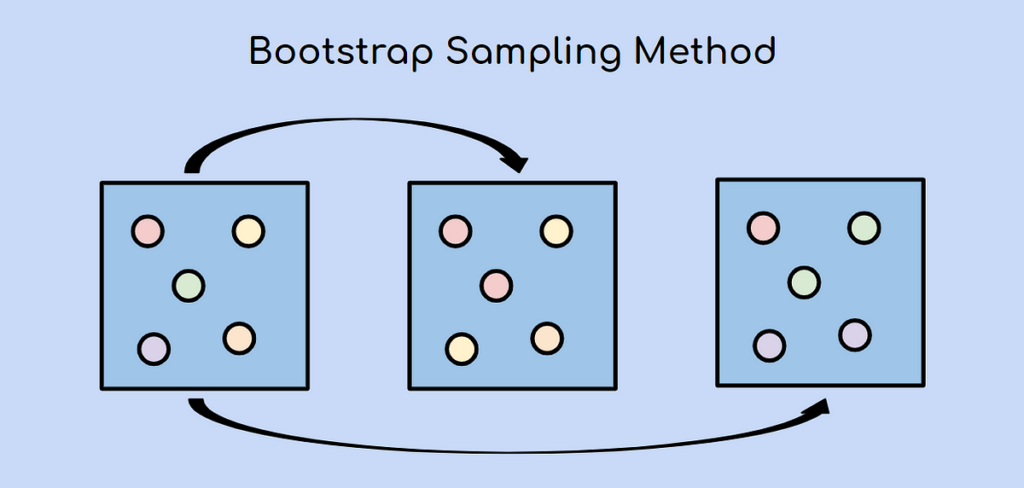
Statisticians can create numerous subsets of that type by resampling, simulating datasets that closely resemble the population. These surrogate datasets serve the purpose of examining the variability and uncertainty related to the relevant measures.
They are commonly employed in conjunction with the bootstrap methodology to estimate the sampling variation of different statistics, including the mean, median, standard deviation, or regression coefficient. By repeatedly calculating the desired statistic on each sample, statisticians can construct confidence intervals, evaluate standard errors, conduct hypothesis tests, and assess the robustness of statistical models.
One significant benefit of employing bootstrap samples is the ability to conduct non-parametric analysis. This approach enables the estimation of statistical properties directly from the data without depending on specific assumptions regarding the division of the core population. It is especially valuable when dealing with data that deviates from normality or when the data is unidentified.
When Should I Use Bootstrap Statistics?
Bootstrap statistics is a versatile and powerful resampling technique that can be used in various situations. Here are some scenarios where bootstrap statistics can be particularly useful.
Small Sample Sizes
When dealing with limited data, traditional statistical methods may not provide reliable estimates, or assumptions about the data regarding the population may not hold. In such cases, bootstrap statistics can help overcome these limitations by generating multiple samples and estimating parameters or conducting hypothesis tests without relying on specific distributional assumptions.
Non-normal Data
Many statistical methods assume that the data follow a normal division. However, real-world data often deviate from this assumption. This statistics is robust to non-normality and allows for the estimation of parameters, margin of error, and hypothesis testing without relying on distributional assumptions.
Assessing Uncertainty
It provides a direct and intuitive way to assess the uncertainty associated with statistical estimates. By generating several bootstrap subsets, you can obtain a dispersion of the target parameter and estimate its standard error, construct confidence intervals, and determine the variability of the estimate.
Outlier Detection
Bootstrap statistics can be valuable for identifying outliers and influential observations. By resampling the data and estimating the data of interest on each subset, you can assess the stability and robustness of your results, identify potential outliers, and evaluate their impact on the analysis.
Model Validation
When building predictive models, it is crucial to assess their performance and reliability. This statistics can be used for model validation by generating a number of samples, constructing the model on each of them, and evaluating the consistency of the model’s performance among the subsets. This helps estimate prediction error, assess model stability, and improve the generalizability of the model.
Complex Data Structures
Bootstrap statistics can handle complex data structures, such as clustered or dependent data, where traditional methods may not be applicable. By resampling at the appropriate level (e.g., resampling clusters or blocks of data), bootstrap techniques can provide reliable estimates and inferences in the presence of complex data structures.
Machine Learning Applications
Bootstrap methods find applications in machine learning, especially in ensemble methods like bootstrap aggregating (or bagging). Bagging involves training multiple models on different bootstrap samples and combining their predictions to improve overall prediction accuracy and reduce overfitting.
What is the difference between bootstrapping and random sampling?
Bootstrapping and random sampling are two distinct sampling techniques used in statistics. While both involve selecting samples from a population, there are key differences among them:
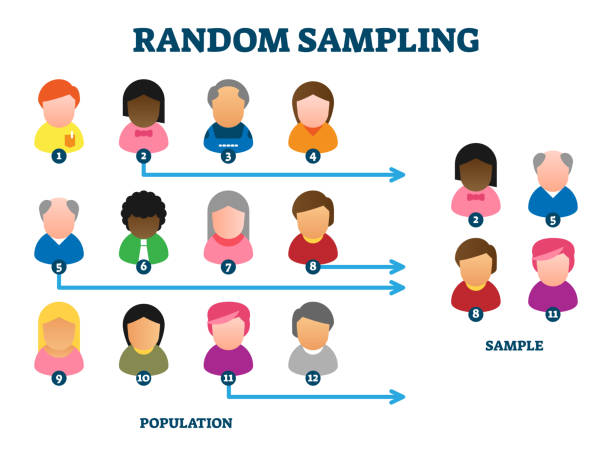
- Sample generation
Random Sampling: It entails the fair and arbitrary selection of observations from the entirety of people. It guarantees that each observation has an equal probability of being chosen, and the process occurs without exchange. The objective is to construct a piece that accurately represents the population and its inherent aspects.
Bootstrapping: This approach involves creating samples by resampling from the primary dataset and employing replacement. This implies that each observation in the original dataset has the chance to be selected multiple times or not at all in each bootstrap sample. The purpose of this method is to estimate the properties of a statistic and evaluate its uncertainty.
- Purpose
Random Sampling: Random sampling is commonly utilized to generate an unbiased and proportional subset that accurately captures the characteristics of the whole. Its primary application lies in cases where the objective is to extend the findings derived from the sample to the entire population through generalization.
Bootstrapping: The primary purpose of this methodology is to estimate the collection of values and draw inferences about the population. It plays a crucial role in assessing the variability and uncertainty.
- Population inference
Random Sampling: By employing random sampling, statisticians can extend the findings derived from a sample to the entirety. The basis for statistical inferences, which involve estimating population parameters or conducting hypothesis tests, relies on the underlying assumption that the sample accurately represents them.
Bootstrapping: Bootstrapping avoids the need for hypotheses regarding this division. Rather than relying on such assumptions, it generates numerous bootstrap samples from the original data and employs them to estimate the characteristics of a statistic. By providing a non-parametric approach to inference, bootstrapping proves valuable in scenarios where assumptions about the population are uncertain or unknown.
- Data requirements
Random Sampling: It requires access to a whole or a sampling frame that accurately represents the population. It is commonly used in surveys and experiments where a random selection of individuals or units is desired.
Bootstrapping: In cases where the sample size is limited, or the assumptions regarding the population dispersion are not met, it becomes highly valuable as it relies on a single sample extracted from the population.
Summing Up
Bootstrap statistics is a powerful resampling technique that has revolutionized the field of statistics. By leveraging the power of resampling, it provides a flexible and reliable approach to estimate parameters, construct confidence intervals, perform hypothesis tests, validate models, and detect outliers. Its ability to handle complex data and relax distributional assumptions has made it an essential tool for statisticians, researchers, and practitioners across various disciplines. As data analysis continues to evolve, bootstrap statistics will undoubtedly remain a valuable asset in the statistician’s toolkit.