Navigating through the complex world of statistics and data analysis, professionals frequently encounter situations where procuring fresh data becomes a costly, time-consuming, or impractical pursuit. Herein, the methodology of Bootstrap resampling emerges as an efficacious approach to employ existing data for generating reliable predictions and solid conclusions.
The objective of this discourse is to illuminate the concept of bootstrap resampling and elucidate how it aids in the process of statistical inference.
Understanding Bootstrap Sampling
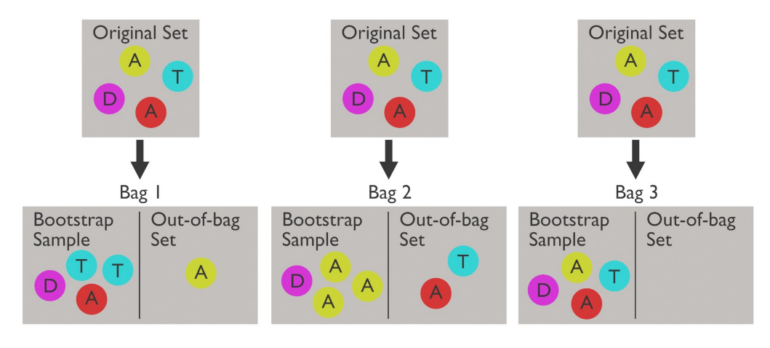
Bootstrap sampling, sometimes referred to as resampling, denotes a statistical strategy encompassing the resampling of data with substitution from a pre-existing data set. Such reiterations of data, termed Bootstrap samples, mirror the original data in terms of size but incorporate arbitrary alterations.
The creation of numerous samples permits researchers to acquire a comprehensive understanding of the primary data and infer robust statistical conclusions.
Establishing Bootstrap Samples: The Procedure
The modus operandi for crafting the samples consists of:
- Substituting during Resampling: Bootstrap sampling entails the random selection of observations from the base dataset with an opportunity for resampling (with substitution). This implies that every observation stands an equal chance for selection in Bootstrap resampling, with certain observations potentially being chosen more than once;
- Preserving Sample Size: A Bootstrap sample is formulated by picking several observations equivalent to the size of the base dataset. While the sample size remains steady, the resampling operation introduces variability by possibly integrating duplicate observations and excluding others.
The aforementioned stages are reiterated numerous times (typically in the thousands) to produce multiple sets. Each sample is a virtual data set that echoes the attributes and patterns located in the primary data set, yet incorporates random variability.
Advantages and Applications of Bootstrap Resampling
The process enables researchers to evaluate diverse parameters of interest like means, variances, and correlations. By repeatedly resampling from the base data, statistical metrics can be determined for every option, facilitating the acquisition of distributions of these estimates. These distributions, in turn, facilitate the calculation of confidence intervals that highlight the uncertainty tied to the parameter being evaluated:
- Hypothesis Testing: The process plays a pivotal role in hypothesis testing, particularly when the premises of traditional tests are violated or unknown. By juxtaposing the distribution of Bootstrap sampling statistics to observed statistics, researchers can appraise the significance of their discoveries and make enlightened decisions regarding hypotheses;
- Model Verification: It assists in verifying predictive models by evaluating their efficiency and consistency. Through resampling pre-existing data, analysts can quantify the uncertainty correlated with model forecasts and examine the stability of the selected model.
Bootstrap sampling proves beneficial in pinpointing outliers within a dataset. By forming bootstrap sets and scrutinizing the consistency of model estimations or resampling statistics, remarkable observations that regularly wield a substantial impact on the results can be singled out.
How is a Bootstrap Set Assembled?
The assembly of a bootstrap set encompasses the subsequent steps:
- Initiate with a Dataset: Begin with a dataset encompassing the observations or data points intended for analysis. This dataset should epitomize the populace or sample from which conclusions are to be drawn;
- Resampling with Substitution: To generate a Bootstrap set, randomly select observations from the base dataset, facilitating replacement. “With replacement” implies that every chosen observation is reinstated into the pool of accessible observations before the next selection. This assures that the sample size mirrors the original dataset;
- Preserving Sample Size: The size of the Bootstrap set should parallel that of the original dataset. This signifies that you sample an equivalent number of observations as the total observations present in the original dataset;
- Repeat the Procedure: To procure dependable estimations, the resampling process should be reiterated numerous times. This involves performing steps 2 and 3 – resampling with substitution and maintaining the sample size – thousands of times. The quantity of iterations hinges on the desired precision level and the complexity of the dataset;
- Analyze Bootstrap Sets: Post the creation of several Bootstrap sets, they can be analyzed to assess parameters, calculate confidence intervals, test hypotheses, evaluate models, or detect outliers.
It’s crucial to acknowledge that the random selection process of Bootstrap allows for variability in every set. This variability mirrors the inherent uncertainty within the data and assists in reflecting the complexity of the underlying populace or sample.
How Does a Bootstrap Set Differ from the Original Sample?
A Bootstrap set differs from the original sample in two principal ways: the selection technique and the presence of variability.
Selection Technique:
- Bootstrap Set: A Bootstrap set is obtained by selecting a subset of observations from the populace or sample of interest using a distinct method of selection (e.g., random sampling, stratified sampling, convenience sampling). The selection of observations in the initial sample typically adheres to a predetermined scheme or strategy;
- Bootstrap Sampling: This is where observations are chosen from the original sample itself with substitution. This denotes that every observation in the original sample has an equal likelihood of being selected for Bootstrap sampling, and some observations may be chosen multiple times. The process is random and does not adhere to a predetermined scheme or strategy beyond maintaining sample size.
Variability
- Baseline Set: A baseline set is a solitary snapshot or realization of a populace or sample of interest. It mirrors specific observations that were chosen at a particular point in time. Estimates and statistics deduced from a baseline sample provide insight into the characteristics of the population or sample, but they do not account for the uncertainty associated with sampling variability;
- Bootstrap samples introduce diversity by resampling from the original set with substitution. Every sample is a replicated dataset that mirrors the size of the original set but incorporates random variation due to the integration of duplicate observations and the exclusion of others.
By creating numerous options, analysts can account for the inherent uncertainty within the data and procure distributions of estimates, thereby allowing them to quantify the variability and uncertainty tied to the original set.
Concluding Thoughts
Bootstrap sampling emerges as a potent instrument for researchers and statisticians to investigate and interpret data, even in circumstances where gathering more data proves challenging.
By resampling from a pre-existing dataset, Bootstrap sampling facilitates dependable estimates, confidence intervals, and enhanced comprehension of the underlying data distribution.